Geometry Tests
Cadcorp SIS Desktop 9.1 spatial testing, including Spatial Filter spatial testing, uses the Open Geospatial Consortium (OGC) Relate method. This measures the dimensions of the nine intersections formed between the interior, boundary and exterior of the two items being compared. The different tests have different rules for which dimension matrices are valid.
Cadcorp SIS Desktop 9.1 spatial tests have a test item, which can be a Spatial Filter object, and one or more candidate items. Each candidate item is compared to the test item using a testing predicate and a testing mode.
The OGC specifies the Dimensionally Extended Nine-Intersection Model (DE-9IM) method for computing the spatial relationships between geometries, see OpenGIS® Implementation Specification for Geographic information - Simple feature access - Part 1: Common architecture
Testing Modes
- Origin
The origin of the candidate item (always a single point) must pass the testing method with the test item.
- Extents
The extents of the candidate item (always a rectangle) must pass the testing method with the test item.
- Geometry
The geometry of the candidate item must pass the testing method with the test item.
Pattern Matrix
The pattern matrix consists of a set of nine pattern-values, one for each cell in the matrix. The possible pattern-values are T, F, *, 0, 1, 2. The meanings of these values are summarised here:
| 0 | An intersection must exist and its maximum dimension must be 0. (Point Intersection). |
| 1 | An intersection must exist and its maximum dimension must be 1. (LineString Intersection). |
| 2 | An intersection must exist and its maximum dimension must be 2. (Area Intersection). |
| T | An intersection must exist, the dimension is irrelevant. |
| F | An intersection must not exist. (Intersection is the empty set). |
| * | It does not matter if an intersection exists or not. |
These values are fully described in the OpenGIS® Implementation Specification for Geographic information - Simple feature access - Part 1: Common architecture.
Testing Predicates
The testing predicates are:
- Contains - Geometry B lies in the interior of Geometry A (the inverse of Within)
- Cross - The Geometries share some but not all interior points, and the dimension of the intersection is less than that of at least one of the Geometries
- Crossed By - The Geometries that are crossed by but not contained by another geometry
- Disjoint - The Geometries have no point in common
- Equal - The Geometries are topologically equal
- Intersects - The Geometries have at least one point in common (the inverse of Disjoint)
- Overlap - The Geometries share some but not all points in common, and the intersection has the same dimension as the Geometries themselves
- Touch - The Geometries have at least one boundary point in common, but no interior points
- Within - Geometry A lies in the interior of Geometry B
Contains
Contains returns T if the second geometry object is completely contained by Geometry A. The boundary and interior of Geometry B are not allowed to intersect the exterior of Geometry A and the geometries need not not be equal.
The Contains predicate returns the exact opposite of the Within predicate.
The Contains pattern matrix (DE-9IM):
[T** *** FF*]
Examples of the Contains predicate:
Pattern matrix of the Contains predicate:
The following Contains predicate matrix shows that the interiors of both Geometries must intersect and that the interior and boundary of Geometry B must not intersect the exterior of Geometry A.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | * |
| Boundary (A) | * | * | * |
| Exterior (A) | F | F | * |
See also: Cross, Crossed By, Disjoint, Equal, Intersects, Overlap, Touch, Within
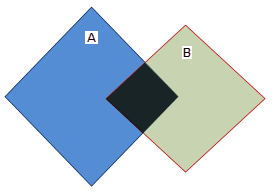
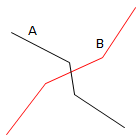
Cross
Cross returns T if the intersection results in a geometry whose dimension is one less than the maximum dimension of the two source items and the interiors of both geometries are intersected.
The Geometries share some but not all interior points, and the dimension of the intersection is less than that of at least one of the Geometries.
If the items are LineString items, they must intersect without being tangential. Otherwise, their interiors must intersect, with the test item going outside the candidate item.
The Cross pattern matrices (DE-9IM):
[0** *** ***] for LineString/LineString, Linestring/MultiLineString and MultiLineString/MultiLineString items
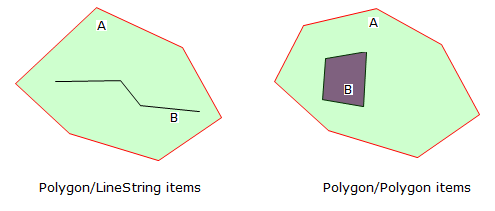
[T*T *** ***] for Polygon/LineString, Polygon/Area and LineString/Area items
[T** *** T**] for LineString/Polygon, LineString/Area and Area/LineString items
Examples of the Cross predicate:
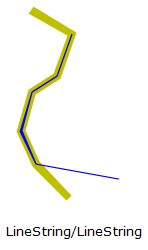
Example 1: LineString/LineString items
Pattern matrix of the Cross predicate for LineString/LineString items:
The following Cross predicate matrix applies to LineString/LineString, Linestring/MultiLineString and MultiLineString/MultiLineString items. The dimension of the intersection of the interiors must be 0, i.e. intersect at a Point. If the dimension of this intersection was 1, i.e. intersect at a LineString, the Cross predicate would return F but the Overlap predicate would return T.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | 0 | * | * |
| Boundary (A) | * | * | * |
| Exterior (A) | * | * | * |
Example 2: LineString/Polygon items
The following Cross predicate matrix applies to MultiPoint/LineString, MultiPoint/MultiLineString, MultiPoint/Polygon, MultiPoint/MultiPolygon, LineString/Polygon and LineString/MultiPolygon items. The interiors must intersect and at least the interior of Geometry A must intersect the exterior of the Geometry B.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | T |
| Boundary (A) | * | * | * |
| Exterior (A) | * | * | * |
See also: Contains, Crossed By, Disjoint, Equal, Intersects, Overlap, Touch, Within
Crossed By
Geometries that are crossed by but not contained by another geometry.
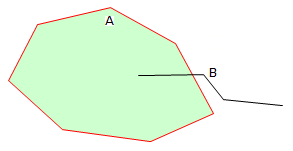
LineString items will be found if they intersect the selected item without being tangential.
Polygon items will be found if their interior intersects with the interior of the selected item and the found item goes outside the selected item.
Example 1: LineString/Polygon items
Example 1: LineString/Linestring items
Note: Crossed By is not included in the Dimensionally Extended Nine-Intersection Model (DE-9IM) specification.
See also: Contains, Cross, Disjoint, Equal, Intersects, Overlap, Touch, Within
Disjoint
Disjoint returns T if the geometries are completely separate, with no point in common and daylight between them.
The Disjoint pattern matrix (DE-9IM):
[FF* FF* ***]
Examples of the Disjoint predicate:
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | F | F | T |
| Boundary (A) | F | F | * |
| Exterior (A) | * | * | * |
See also: Contains, Cross, Crossed By, Equal, Intersects, Overlap, Touch, Within
Equal
Equals returns T if the geometries are equal if they have matching X, Y coordinates.
The Equals pattern matrix (DE-9IM):
[T*F **F FF*]
Examples of the Equals predicate:
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | F |
| Boundary (A) | * | * | F |
| Exterior (A) | F | F | * |
See also: Contains, Cross, Crossed By, Disjoint, Intersects, Overlap, Touch, Within
Intersects
Intersect returns T if the items are not disjoint, they must have a point in common. This is the fastest, and most common test. The Geometries have at least one point in common (the inverse of Disjoint).
The Intersect pattern matrices (DE-9IM):
[T** *** ***] if the interiors of both geometries intersect
[*** *T* ***] if the boundaries of either geometry intersect
[*** T** ***] if the boundary of the first geometry intersects the boundary of the second geometry
[*T* *** ***] if the boundary of the first geometry intersects the interior of the second geometry
Examples of the Intersect predicate:
Example 1: Interiors of both geometries intersect
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | * |
| Boundary (A) | * | * | * |
| Exterior (A) | * | * | * |
Example 2: If the boundaries of either geometry intersect
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | * | * | * |
| Boundary (A) | * | T | * |
| Exterior (A) | * | * | * |
Example 3: The boundary of Geometry A intersects the interior of Geometry B
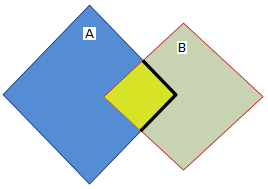
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | * | * | * |
| Boundary (A) | T | * | * |
| Exterior (A) | * | * | * |
See also: Contains, Cross, Crossed By, Disjoint, Equal, Overlap, Touch, Within
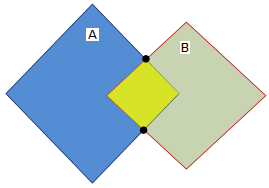
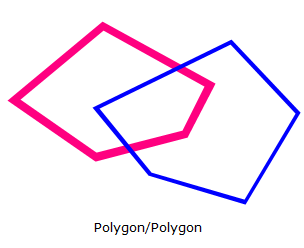
Overlap
Overlap returns T if the geometries have some but not all points in common, they have the same dimension, and the intersection of the interiors of the two geometries has the same dimension as the geometries themselves.
If the two items are LineString items, then they must be tangential, and neither should contain the other. Otherwise, their interiors must intersect, with neither containing the other.
The Overlap pattern matrix (DE-9IM):
[1*T *** T**] for LineString/LineString, Linestring/MultiLineString and MultiLineString/MultiLineString items
[T*T *** T**] for Polygon/Polygon, MultiPoint/MultiPoint and MuliPolygon/MultiPolygon items
Examples of the Overlap predicate:
Example 1: LineString/LineString type items
Pattern matrix of the Overlap predicate for LineString/LineString items:
The following Overlap predicate matrix applies to LineString/LineString, Linestring/MultiLineString and MultiLineString/MultiLineString items. In this case the intersection of the geometries must result in a geometry that has a dimension of 1, i.e. another LineString item. If the dimension of the intersection of the interiors had resulted in 0, i.e. a Point, then the Overlap predicate would return F with the Cross predicate returning T.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | 1 | * | T |
| Boundary (A) | * | * | * |
| Exterior (A) | T | * | * |
Note: The value 1 means an intersection exists and its maximum value is 1.
Example 2: Polygon/Polygon/Point items
Pattern matrix of the Overlap predicate for Polygon/Polygon/Point items:
The following Overlap predicate matrix applies to Polygon/Polygon/Point items. If the interior of both geometries intersects the others interior and exterior then the Overlap predicate returns T.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | T |
| Boundary (A) | * | * | * |
| Exterior (A) | T | * | * |
See also: Contains, Cross,Crossed By, Disjoint, Equal, Intersects, Touch, Within
Touch
Touch returns T if the items' interiors are disjoint and their boundaries intersect. The Geometries must have at least one boundary.
Touch will return T in either of the following cases:
- none of the Points common to both geometries intersect the interiors of both geometries. At least one geometry must be a LineString, Polygon, MultiLineString or MultiPolygon.
- either of the geometries' boundaries intersect or only one of the geometry's interiors intersects the other's boundary.
The Touch pattern matrix (DE-9IM):
[FT* *** ***] the boundary of one geometry intersects the interior of the other
[F** T** ***] the boundary of one geometry intersects the interior of the other but the interiors do not intersect
[F** *F* ***] the boundaries of both geometries intersect but the interiors do not
Examples of the Touch predicate:
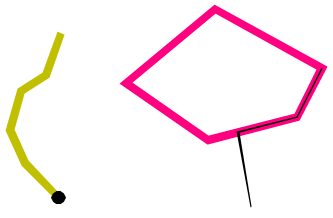
Pattern matrix of the Touch predicate
The boundary of one geometry intersects the interior of the other:
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | F | T | T |
| Boundary (A) | * | * | * |
| Exterior (A) | * | * | * |
The boundary of one geometry intersects the interior of the other but the interiors do not intersect:
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | F | * | * |
| Boundary (A) | T | * | * |
| Exterior (A) | * | * | * |
The boundaries of both geometries intersect but the interiors do not:
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | F | * | * |
| Boundary (A) | * | T | * |
| Exterior (A) | * | * | * |
See also: Contains, Cross, Crossed By, Disjoint, Equal, Intersects, Overlap, Within
Within
Within returns T if the interior of Geometry A is strictly inside Geometry B.
The interior or boundary of Geometry A must not intersect the exterior of Geometry B and Geometry A must not equal Geometry B.
the Within pattern matrix (DE-9IM):
[T*F **F ***]
Examples of the Within predicate:
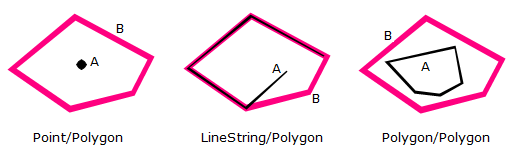
Pattern matrix of the Within predicate:
The following Within predicate matrix shows that the interiors of both geometries must intersect and that the interior and boundary of Geometry A must not intersect the exterior of Geometry B.
| Interior (B) | Boundary (B) | Exterior (B) | |
| Interior (A) | T | * | F |
| Boundary (A) | * | * | F |
| Exterior (A) | * | * | * |
See also: Contains, Cross, Crossed By, Disjoint, Equal, Intersects, Overlap, Touch